NÚMEROS ENTEROS
OBJETIVOS
Reconocer y utilizar los números enteros en situaciones cotidianas. Identificar números en la recta entera. Representar números en la recta entera. Comparar y ordenar números enteros Identificar las coordenadas cartesianas de puntos.CRITERIOS DE EVALUACIÓN.
Reconoce y utiliza los números enteros en situaciones cotidianas. Identifica números en la recta entera. Representa números en la recta entera. Comprar y ordena números enteros. Identifica la coordenadas cartesianas de puntos. Representa un punto a partir de sus coordenadas. .
.
NÚMEROS ENTEROS.
.
Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, …), los negativos de los números naturales (…, −3, −2, −1) y al 0.
Los enteros negativos, como −1 o −3 (se leen «menos uno», «menos tres», etc.), son menores que todos los enteros positivos (1, 2, …) y que el cero.
Para resaltar la diferencia entre positivos y negativos, a veces también se escribe un signo «más» delante de los positivos: +1, +5, etc. Cuando no se le escribe signo al número se asume que es positivo.
El conjunto de todos los números enteros se representa por la letra  = {…, −3, −2, −1, 0, +1, +2, +3, …}
= {…, −3, −2, −1, 0, +1, +2, +3, …}
Por lo tanto, los números enteros son aquellos que no tienen parte decimal (es decir que 3,28, por ejemplo, no es un número entero).
.
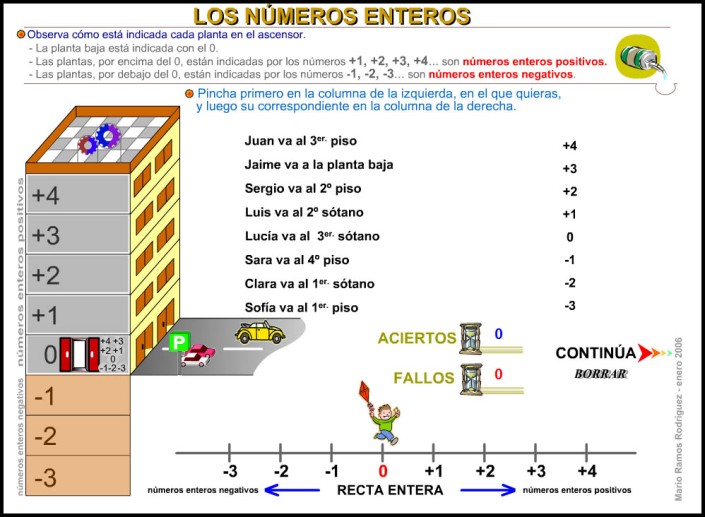
Pulsa en la siguiente imagen y comienza a practicar con los números enteros (y recuerda no es lo mismo tener 15 € que -15 €)
.
Para comenzar un poquito de historia, que no viene mal del todo…..
.
Desde hacía mucho tiempo, los chinos utilizaban bastoncillos de bambú o de madera para representar los números y realizar, en especial, cálculos comerciales de una manera práctica, pero también para tratar cuestiones relacionadas con los aumentos y disminuciones de magnitudes, o con distancias recorridas en sentidos opuestos; esos bastoncillos eran negros o rojos según que representaran cantidades positivas o negativas, de acuerdo con una atribución del color que es justamente la opuesta a la empleada en la contabilidad occidental.
Los matemáticos hindúes del siglo VI mencionan también el uso de números negativos para tratar este tipo de problema.
Los antiguos griegos, por el contrario, rechazaron que pudieran existir tales números.
En Europa medieval, los árabes dieron a conocer los números negativos de los hindúes, que en el siglo XII se utilizaban ya ocasionalmente para designar las pérdidas en el análisis de cuestiones financieras.
Durante el Renacimiento, el manejo práctico de esos números en la contabilidad y otros contextos ayudó a su lenta introducción en las matemáticas.
El alemán Michael Stifel (1487-1567), monje agustino convertido al protestantismo y amigo personal de Lutero, fue uno de los primeros en admitir el uso de coeficientes negativos para el estudio de las ecuaciones cuadráticas y divulgó el uso del signo menos “―“ para designar la resta; de hecho, los signos + y ― estaban ya en uso entre los comerciantes alemanes del siglo XV para indicar el exceso o el defecto de mercancías en los almacenes.
Con todo, la consideración de las cantidades negativas como correspondientes a números matemáticamente legítimos alcanzó aceptación general hasta el siglo XVIII, cuando los números negativos empezaron a ser entendidos como opuestos de los positivos.
En la matemática moderna el conjunto de los números enteros (Z) abarca todos los enteros tanto negativos como positivos, y llega hasta el infinito hacia ambos lados de una recta numérica, por tanto, en rigor no existe un comienzo, salvo que como tal se considere el CERO (el cual agregado al conjunto de los números naturales forma el conjunto de los Cardinales).
.
Además de todo lo expuesto tampoco podemos obviar el hecho de que los números enteros nos sirven igualmente para establecer la altura de un monumento o de un elemento natural.
Así, por ejemplo, podemos hablar de que el Mulhacén es el pico más alto que existe en la Península Ibérica pues está situado a 3.478 metrossobre el nivel del mar mientras que el Teide es el más alto de España al conseguir alcanzar los 3.718 metros.
Los números enteros negativos tienen diversas aplicaciones prácticas.
Con ellos se puede señalar una temperatura bajo cero (“En estos momentos, la temperatura en Teruel es de -10º”) o una profundidad bajo el nivel del mar (“El barco hundido fue hallado a -135 metros”).
.
Después de esta explicación podemos animarnos un poco viendo un video que nos explica qué son los NÚMEROS NATURALES.
Pulsar sobre la imagen.
.
OPERACIONES CON NÚMEROS ENTEROS
. Una vez que ya conocemos qué son los números enteros , vamos a ver cómo podemos usarlos en los problemas de la vida cotidiana. . .Suma de números enteros
1. Si los números enteros tienen el mismo signo, se suman los valores absolutos y al resultado se le coloca el signo común.
3 + 5 = 8
(−3) + (−5) = − 8
2. Si números enteros son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le coloca el signo del número de mayor valor absoluto.
− 3 + 5 = 2
3 + (−5) = − 2
Propiedades de la suma de números enteros
1. Asociativa: (a + b) + c = a + (b + c) (2 + 3) + (− 5) = 2 + [3 + (− 5)] 5 − 5 = 2 + (− 2) 0 = 0 . 2. Conmutativa: a + b = b + a 2 + (− 5) = (− 5) + 2 − 3 = − 3 3. Elemento neutro: a + 0 = a (−5) + 0 = − 5 4. Elemento opuesto a + (-a) = 0 –> 5 + (−5) = 0 –> −(−5) = 5 . . Ahora toca comprobar lo que hemos entendido. Pulsa la siguiente imagen. . .
.Resta de números enteros
.
La diferencia de los números enteros se obtiene sumando al minuendo el opuesto del sustraendo.
a – b = a + (-b)
7 − 5 = 2
7 − (−5) = 7 + 5 = 12
Propiedades de la resta de números enteros
1. No es Conmutativa:
a – b ≠ b – a
5 − 2 ≠ 2 − 5
.
.
Y ahora a comprobar nuestros conocimientos con las sumas y restas de números enteros.
.
Multiplicación de números enteros
.
La multiplicación de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
Regla de los signos

2 · 5 = 10
(−2) · (−5) = 10
2 · (−5) = − 10
(−2) · 5 = − 10
.
.
Vamos a jugar!!!!!!
.
.
Propiedades de la multiplicación de números enteros
1. Asociativa:
(a · b) · c = a · (b · c)
(2 · 3) · (−5) = 2· [(3 · (−5)]
6 · (−5) = 2 · (−15)
-30 = -30
2. Conmutativa: a · b = b · a 2 · (−5) = (−5) · 2 -10 = -10
3. Elemento neutro: a ·1 = a (−5)· 1 = (−5)
5. Distributiva: a · (b + c) = a · b + a · c
(−2)· (3 + 5) = (−2) · 3 + (−2) · 5
(−2)· 8 =- 6 – 10
-16 = -16
6. Sacar factor común: a · b + a · c = a · (b + c) (−2) · 3 + (−2) · 5 = (−2) · (3 + 5)
.
.
.
División de números enteros
La división de dos números enteros es otro número entero, que tiene como valor absoluto el cociente de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
10 : 5 = 2
(−10) : (−5) = 2
10 : (−5) = − 2
(−10) : 5 = − 2
Propiedades de la división de números enteros
1. No es Conmutativo:
a : b ≠ b : a
6 : (−2) ≠ (−2) : 6
.
Potencia de números enteros
.
La potencia de exponente natural de un número entero es otro número entero, cuyo valor absoluto es el valor absoluto de la potencia y cuyo signo es el que se deduce de la aplicación de las siguientes reglas:
1. Las potencias de exponente par son siempre positivas.
2. Las potencias de exponente impar tienen el mismo signo de la base.
Propiedades
a0 = 1 ·
a1 = a
am · a n = am+n
(−2)5 ·(−2)2 = (−2)5+2 = (−2)7 = −128
am : a n = am – n
(−2)5 : (−2)2 = (−2)5 – 2 = (−2)3 = −8
(am)n = am · n
[(−2)3]2 = (−2)6 = 64
an · b n = (a · b) n
(−2)3 · (3)3 = (−6) 3 = −216
an : b n = (a : b) n
(−6)3 : 3 3 = (−2)3 = −8
Potencias de exponente entero negativo
.
Raíz cuadrada de un número entero
Las raíces cuadradas de números enteros tienen dos signos: positivo y negativo.

El radicando es siempre un número positivo o igual a cero, ya que se trata del cuadrado número.
.
Operaciones combinadas con números enteros
.
Prioridades en las operaciones
1º.Efectuar las operaciones entre paréntesis, corchetes y llaves..
2º.Calcular las potencias y raíces.
3º.Efectuar los productos y cocientes.
4º.Realizar las sumas y restas.
LA RECTA ENTERA. COMPARACIÓN DE NÚMEROS ENTEROS
.
.
Para comparar dos números sobre una recta, hay que mirar la posición de ambos sobre ella
- El número menor será el que se encuentre más a la izquierda.
- El número mayor será el que se encuentre más a la derecha.
.
.
.COORDENADAS CARTESIANAS.
.
Las coordenadas cartesianas se pueden usar para decir dónde estás exactamente en un mapa o gráfico
Con las coordenadas cartesianas señalas un punto en un gráfico dando la distancia de lado y hacia arriba:
 |
| El punto (12,5) está 12 unidades a la derecha y 5 arriba. |
Ejes X e Y
| La dirección izquierda-derecha (horizontal) se suele llamar X …… y arriba-abajo (vertical) se suele llamar Y.Las líneas de referencia (desde donde se miden distancias) se llaman ejes.
Hay un eje X y un eje Y.
|  |
| El eje X pasa por cero horizontalmente El eje Y pasa por cero verticalmente |
.
Ahora os dejamos un enlace para que podáis ver mucho mejor cómo se localizan los puntos de las coordenadas dentro de unos ejes de coordenadas.
.
Direcciones
| Cuando x (la primera coordenada) aumenta, el punto se mueve a la derecha. (Si disminuye, el punto va a la izquierda.) | |
| Cuando y (la segunda coordenada) aumenta, el punto se mueve arriba. (Si disminuye, el punto va abajo.) |
.
.
Escribir coordenadas
Las coordenadas siempre se escriben en el mismo orden: la dirección horizontal primero, después la vertical. Esto se llama un “par ordenado”.
Y normalmente los números se separan con una coma, y se rodean con paréntesis así: (3,2)
Ejemplo: (4,9) significa 4 unidades a la derecha y 9 arriba
Ejemplo: (0,5) significa 0 unidades a la derecha y 5 arriba. En otras palabras, sólo 5 unidades arriba.
| Se llaman cartesianas porque las ideó el matemático y filósofo René Descartes a quien también se llamaba Cartesio. Es famoso por la frase “Pienso, luego existo”. |
.
.
Cuadrantes
¿Qué pasa cuando x o y es negativo? ¡Pues que empezamos en cero y vamos en la dirección contraria!
Esto significa que es posible tener combinaciones como x positivo e y negativo, o los dos negativos. De hecho hay cuatro combinaciones, y en un gráfico se llaman cuadrantes:
| X (horizontal) | Y (vertical) | Ejemplo | Cuadrante |
|---|---|---|---|
| Positivo | Positivo | (3,2) | I |
| Negativo | Positivo | (-4,3) | II |
| Negativo | Negativo | (-2,-1) | III |
| Positivo | Negativo | (2,-3) | IV |
| La palabra cuadrante viene de cuad que significa cuatro. Por ejemplo, cuatro bebés que nacen a la vez se llaman cuatrillizos, y un animal de cuatro patas se llama cuadrúpedo) |
Aquí tienes los cuatro cuadrantes en un gráfico:
 |
Ejemplo: el punto “A” (3,2) está 3 unidades a la derecha y 2 arriba. Como x e y son positivos, el punto está en el “cuadrante I”
Ejemplo: el punto “C” (-2,-1) está 2 unidades horizontalmente en dirección negativa,
y 1 abajo (también dirección negativa). Como x e y son los dos negativos, el punto está en el “cuadrante III”
y 1 abajo (también dirección negativa). Como x e y son los dos negativos, el punto está en el “cuadrante III”
.
.
El origen
El punto (0,0) tiene el nombre especial de “el origen”, y a veces se le llama con la letra “O”.
.
.
Dimensiones: 1, 2, 3 y más…
Piensa en esto:
| 1 | En la línea de números sólo se puede ir a izquierda o derecha, así que cualquier posición se indica con un número |
|---|---|
| 2 | Las coordenadas cartesianas indican direcciones izquierda-derecha y arriba-abajo, así cualquier posición se indica con dos números |
| 3 | ¿Cómo señalamos un punto en el mundo real (como la punta de tu nariz)? Necesitamos indicar izquierda-derecha, arriba-abajo y delante-detrás, eso son tres números, ¡o 3 dimensiones! |
Y se pueden usar coordenadas cartesianas para localizar puntos en 3 dimensiones como en este ejemplo:
 |
| Aquí el punto (-4,-4,5) se indica en coordenadas cartesianas tridimensionales. |
.